
| 优点 | 易编码实现 |
| 缺点 | 在大数据集上可能较慢 |
| 适用数据类型 | 数值型, 标称型 |
基础概念1. 关联分析(association analysis)从大规模数据集中寻找物品间的隐含关系, 这些关系可以有两种形式: 频繁项集和关联规则. 首先要找到频繁项集, 然后才能获得关联规则.
2. 频繁项集(frequent item sets), 指经常出现在一块的物品的集合.
3. 关联规则(association rules), 暗示两种物品之间可能存在很强的关系.
4. 支持度(support), 项集的支持度指数据集中包含该项集的记录所占的比例.
5. 可信度/置信度(confidence) 定义的规则的适用度. 如我们定义了一条规则 {尿布} -> {葡萄酒}, 则此规则的可信度的计算公式为: 支持度({尿布, 葡萄酒} / 支持度({尿布})". 如果计算结果为 0.75, 表示对于包含"尿布"的所有记录, 我们的规则对其中 75% 的记录都适用.
6. Apriori原理如果某个项集是频繁的, 那么它的所有子集也是频繁的. 即如果一个集合不是频繁的, 那么所有包含它的集合也不是频繁的; 据此可以避免项集数目的指数增长, 从而在合理时间内计算出频繁项集.
算法描述 1. Apriori 算法得到频繁项集 (0). Apriori 算法是根据 Apriori原理发现频繁集的一种方法. (1). 生成所有单个物品的项集列表 (2). 去掉不满足最小支持度的项集 (3). 剩下的项集, 假设每个项集中元素个数为 k, 则两两组合, 生成包含元素个数为 k+1 的项集集合 (4). 重复(2)->(3), 直至(2)进行完成后, 所有的项集都被去掉为止
2. 由频繁项集挖掘关联规则
(0). 如果某条规则不满足最小可信度要求, 那么该规则的所有子集也不满足最小可信度要求. 如, 假设规则{0, 1, 2}->3 不满足最小可信度要求, 那么任何左部为 {0, 1, 2} 子集的规则也不会满足最小可信度要求.(1). 从一个频繁项集创建一个规则列表, 其中规则右部只包含一个元素(2). 对这些规则进行测试, 去掉所有不满足最小可信度的规则(3). 假设剩余规则右部包含 k 个元素, 合并剩余规则来创建新的规则列表, 其中规则右部包含 k+1 个元素(4). 重复 (2) -> (3), 直至 (2) 进行完后, 所有规则被去掉为止算法流程图
1. Apriori 算法得到频繁项集
2. 由频繁项集挖掘关联规则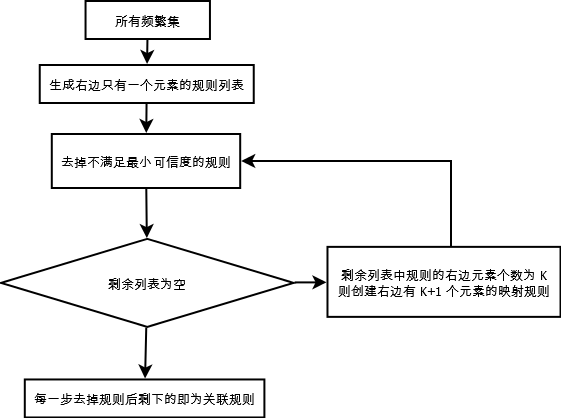 代码
代码
# -*- coding: utf-8 -* from numpy import *# 载入数据def loadDataSet(): return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]# 创建大小为 1 的所有候选项集的集合, 如 { {0}, {1}, {2}...}# Apriori 算法首先创建 C1, 根据最小支持度从 C1 中得到 L1; # 然后 L1 组合成 C2, 根据最小支持试从 C2 得到 L2; # 然后 L2 组合成 C3... def createC1(dataSet): C1 = [] for transaction in dataSet: for item in transaction: if not [item] in C1: C1.append([item]) C1.sort() # 这里使用 frozenset 而不直接用 set, 是因为之后要将这些项集作为字典键值使用 return map(frozenset, C1)# 将 Ck 中没有达到最小支持度(minSupport) 的选项去掉# 返回值 retList 为达到最小支持度的项集# 返回值 supportData 为各个项集的支持度def scanD(D, Ck, minSupport): ssCnt = {} # 创建 Ck 中每个项集及其在 D 中出现的次数的 map for tid in D: for can in Ck: if can.issubset(tid): if not ssCnt.has_key(can): ssCnt[can]=1 else: ssCnt[can] += 1 numItems = float(len(D)) retList = [] supportData = {} for key in ssCnt: support = ssCnt[key]/numItems # 计算支持度 if support >= minSupport: # 只取支持度大于 minSupport 的项集 retList.insert(0,key) supportData[key] = support return retList, supportData# 根据频繁项集 Lk 和 元素个数 k, 生成 Ck# 如由{ {0}, {1}, {2}}, 生成 { {0, 1}, {0, 2}, {1, 2}}def aprioriGen(Lk, k): #creates Ck retList = [] lenLk = len(Lk) for i in range(lenLk): for j in range(i+1, lenLk): L1 = list(Lk[i])[:k-2] # 取前 k-1 个元素作为一个 list L2 = list(Lk[j])[:k-2] # 取前 k-1 个元素作为一个 list L1.sort(); L2.sort() # 如果两个集合前 k-2 个元素相同, 就把它们合并成一个长度为 k 的集合 # 它们最后的元素肯定是不同的 if L1==L2: retList.append(Lk[i] | Lk[j]) return retList# 根据数据集 dataSet 和 最小支持度 minSupport 创建频繁集# 返回值 L 包含在每一步时所取到的频繁集def apriori(dataSet, minSupport = 0.5): C1 = createC1(dataSet) D = map(set, dataSet) L1, supportData = scanD(D, C1, minSupport) L = [L1] k = 2 # 当新取到的集合中大于最小支持度的项集为空时结束 while (len(L[k-2]) > 0): Ck = aprioriGen(L[k-2], k) Lk, supK = scanD(D, Ck, minSupport) # 由 Ck 得到 Lk supportData.update(supK) # 字典的 update 方法, 将 supK 添加到 supportData L.append(Lk) k += 1 return L, supportData# 参数 L 为频繁项集列表# 参数 supportData 为频繁项集对应的支持度# 参数 minConf 为最小可信度# 返回值为创建好的 规则列表def generateRules(L, supportData, minConf=0.7): bigRuleList = [] # 只取两个或更多元素的集合 # 集合中只有一个元素, 就谈不上映射规则了 for i in range(1, len(L)): for freqSet in L[i]: # 创建只包含单个元素的集合的列表 H1 # 如 freqSet 为 {0, 1, 2}, 则 H1 为 { {0}, {1}, {2}} H1 = [frozenset([item]) for item in freqSet] if (i > 1): rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf) else: # 如果项集中只有两个元素, 则直接计算可信度 calcConf(freqSet, H1, supportData, bigRuleList, minConf) return bigRuleList # 计算可信度, 返回满足最小可信度的规则列表, 由 brl 存放规则及可信度# 返回值 prunedH 为满足条件的规则右边集合列表def calcConf(freqSet, H, supportData, brl, minConf=0.7): prunedH = [] for conseq in H: conf = supportData[freqSet]/supportData[freqSet-conseq] # 计算可信度 if conf >= minConf: brl.append((freqSet-conseq, conseq, conf)) # 保存规则及可信度 prunedH.append(conseq) return prunedH# 递归合并规则右边# 参数 freqSet 为# 参数 H 为可以出现在规则右边的元素列表def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7): m = len(H[0]) if (len(freqSet) > (m + 1)): # 尝试进一步合并 Hmp1 = aprioriGen(H, m+1) # 创建 Hm+1 条新候选规则 Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf) if (len(Hmp1) > 1): # 如果不止一条规则满足, 则尝试进一步合并规则右边 rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)if __name__ == "__main__": dataSet = loadDataSet() L, supportData = apriori(dataSet, minSupport=0.5) rules = generateRules(L, supportData, minConf=0.7) for rule in rules: print "规则:", rule[0], "->", rule[1], "可信度:", rule[2] 运行结果
说明
本文为《Machine Leaning in Action》第十一章(Association analysis with the Apriori algorithm)读书笔记, 代码稍作修改及注释.好文参考
1.《》2.《》